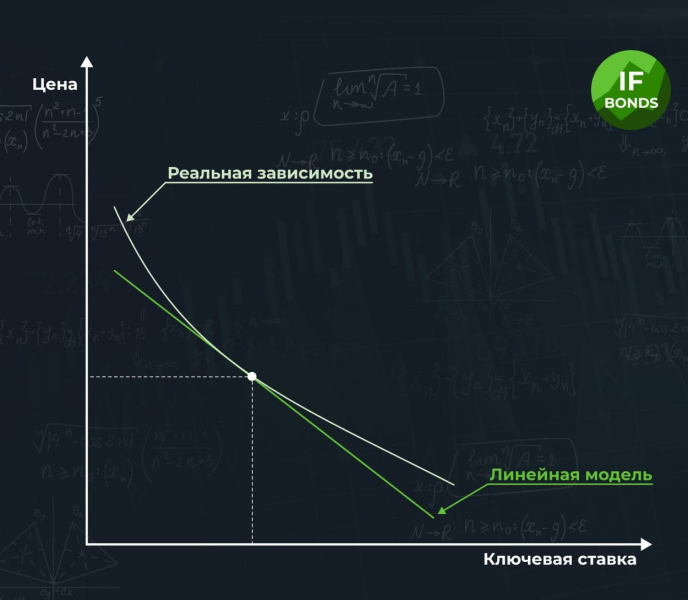
Математики для описания зависимости одной величины от другой используют понятие функции. Из школьной программы даже троечники помнят, что существуют разные виды функций: например, линейная, экспоненциальная. Самая простая функция — линейная. Графически ее можно представить как прямую линию.
Любую закономерность можно описать математической функцией. Проблема только в том, что далеко не все зависимости линейны. Не линейна и цена облигации. Она зависит от изменения ключевой ставки, а это тоже некая математическая функция. Если представить ее графически, то получится выпуклая линия.
Как рассчитать функцию цены облигации?
Обычно инвесторы не заморачиваются с подобными громоздкими расчетами, а используют показатели дюрации. Наиболее распространенным является показатель модифицированной дюрации. Он показывает, на сколько изменится цена облигации при изменении ключевой ставки на 1%.
Допустим, у нас есть облигация с модифицированной дюрацией 1,5 года. Ключевая ставка 8%. Если ставку поднимут до 15%, то цена изменится на -1,5*(0,15-0,08)*100% = -10,5%.
Таким образом, ожидая роста ставок на рынке, стоит присматриваться к облигациям с меньшей дюрацией. А при понижении ставок покупать облигации с большей дюрацией.
Загвоздка в том, что дюрация — линейный показатель. Но при незначительных колебаниях ключевой ставки, а также если ваш инвестиционный портфель не очень велик, дюрация вполне подходит, а точные расчеты излишни.
Зачем оценивать выпуклость облигации?
Проблемы начинаются при резких и более заметных колебаниях ключевой ставки, когда линейные показатели начинают давать заметную погрешность. В этом случае в ход идет показатель выпуклости облигации. Еще этот показатель часто называют конвекцией облигации.
Как посчитать выпуклость облигации?
Выпуклость — это мера кривизны функции. Показатель выпуклости облигации — это производная от модифицированной дюрации облигации. Переводя с математического на русский, выпуклость показывает, как изменяется дюрация облигации в зависимости от изменения ключевой ставки.
Этот показатель можно найти на сайтах-агрегаторах, например rusbonds, cbonds.
Таким образом, для снижения погрешности вычислений используется два параметра одновременно — дюрация и выпуклость.
Влияние выпуклости на изменение цены будет рассчитываться по формуле:
0,5*(изменение ставки)2*Выпуклость*100%
Например, модифицированная дюрация облигации 1,5 года. Выпуклость облигации — 3. Ждем роста ключевой ставки с 8% до 15%. Тогда изменение цены будет рассчитываться вот так:
-
влияние дюрации -1,5*(0,15-0,08)*100% = -10,5%
-
влияние выпуклости 0,5*(0,15-0,08)2*3*100% = 0,735%
-
изменение цены = -10,5%+0,735% = -9,765%
А если считать не хочется?
Тогда используем правило: если есть две облигации с одинаковым кредитным риском и одинаковым уровнем доходности, то выбирать лучше ту, у которой дюрация меньше.
Но что, если и дюрации совпадают? Вот тогда можно сравнить еще и значения выпуклости. Чем выше показатель выпуклости, тем меньше цена будет реагировать на колебания рыночных процентных ставок. На стадии роста ключевой ставки такая облигация будет медленнее терять свою стоимость, а на стадии понижения — быстрее отыгрывать падение.
Правда, все это актуально при заметных колебаниях процентных ставок. На стабильном рынке не стоит придавать особого значения показателю выпуклости. Более того, рынок — не дурак: за большую выпуклость придется заплатить меньшей доходностью.
Аналитик Людмила Рокотянская, редактор Никита Марычев.
InvestFuture.ru
Спасибо за интерес к публикациям на сайте!